Coulomb’s Law (Electric Force)
The electrostatic force acts between all charged particles and is either attractive or repulsive.
The magnitude of the force F between the charges is directly proportional to the product of both charges $Q_1$ and $Q_2$ and directly proportional to the inverse of the square distance r between the centres of the charges.
Note: In physics literature, the symbol for proportionality is different in German ($\sim$) and English ($\propto $).
Opposite charges (attract)
Like negative charges (repel)
Like positive charges (repel)
$$F \propto \frac{Q_1 Q_2}{r^2}$$
Which can be written as
$$F = k \cdot \frac{Q_1 Q_2}{r^2}$$
Experimentally the proportionality constant k was found to be:
$$k = \frac{1}{4\pi \epsilon_0}$$
where $\epsilon_0$ is the permittivity of free space and $\epsilon_0 = 8.854 \cdot 10^{-12} F m^{-1}$
So, Coulomb’s Law becomes:
$$F = \frac{1}{4\pi \epsilon_0} \frac{Q_1 Q_2}{r^2}$$
some symbols explained
F is force in Newtons (N)
Q is the charge in Coulomb (C)
r is the distance from the centre of mass in metres (m)
$\epsilon_0$ is the permittivity of free space and $\epsilon_0 = 8.854 \cdot 10^{-12} F m^{-1}$ . Where the unit farad, F, is the name given to coulomb per volt.
So, $1F = 1\frac{C}{V}$ or $1F = 1CV^{-1}$
simulation of Coulomb’s Law
Electric fields
radial field
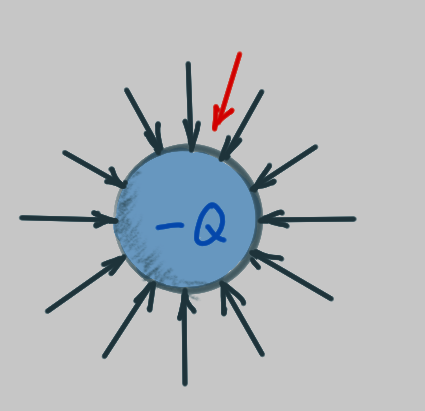
The red vectors are meant to show the magnitude of the forces on a positive test charge in the electric field. A greater distance between the field lines means a weaker force.
uniform field
Electric field strength at any point in an electric field
We now know that the field strength E acting on a positive charge placed in an electric field is defined by the equation
$$E= \frac{F}{Q}$$
So to find the field strength near a point charge (producing a radial field) we have to picture a positive test charge (q) placed in the field and work out the force per unit charge on it. We can find this from Coulomb’s law.
$$F = k \cdot \frac{Q q}{r^2}$$
and
$$F = qE$$
Combining both equations:
$$qE = k \cdot \frac{Q q}{r^2}$$
which simplifies to
$$E = k \cdot \frac{Q}{r^2}$$ where $k = \frac{1}{4\pi \epsilon_0}$ and $\epsilon_0 = 8.854 \cdot 10^{-12} F m^{-1}$ (usually stored in calculators).
Remember that the electric field strength is a vector quantity. The direction of the field is in the same direction of the force on a positive charge.
Electric potential energy
LEIFIphysik - careful with the different symbols in German and English.
If the work done to move one coulomb of electric charge between two points is one joule, then the potential difference between these two points is one volt.
This means $$1V = 1 \frac{J}{C}$$
The formula is
$$ W = Q \cdot V $$ or
$$ V = \frac{W}{Q}$$
Exercise in LEIFIPhysik in German
Note: in LEIFIPhysik 1C = 1As (ampere second)