Construct a Square Root

Factors

Say we want to draw a line segment with length equal to $\sqrt{12}$.

We know that $3 \cdot 4 = 12$.

draw a line the length of the sum of the two factors

find the midpoint of the line segment

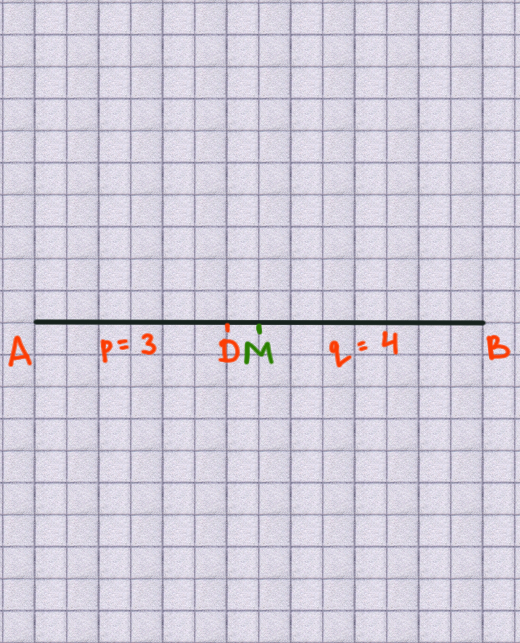
draw a circle

draw a with centre M and radius $r = \overline{MA}$ (or $\overline{MB}$ )

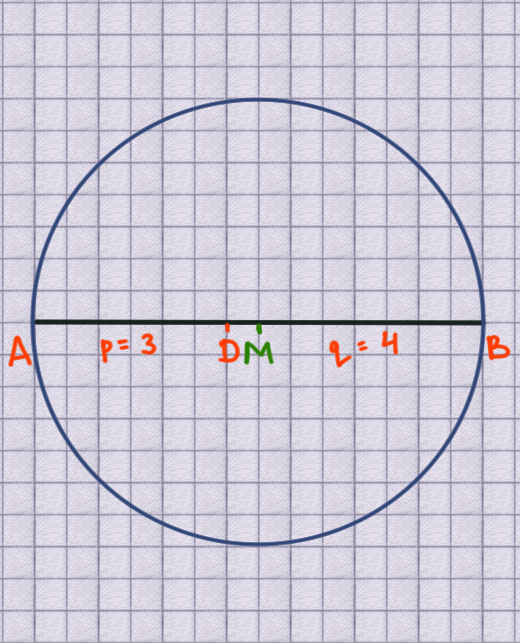
Why a circle?

There is a theorem that states that the angle formed from a point on the arc of a semicircle between the endpoints of the diameter is always a right-angle. In German this is known as Der Thaleskreis.

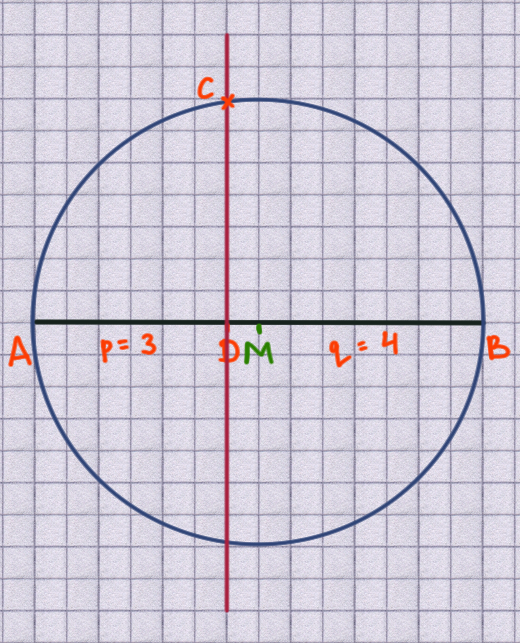
construct a perpendicular

construct a perpendicular through the point D on the line segment AB.

mark point C

draw triangle

this step is not really necessary to find the length.

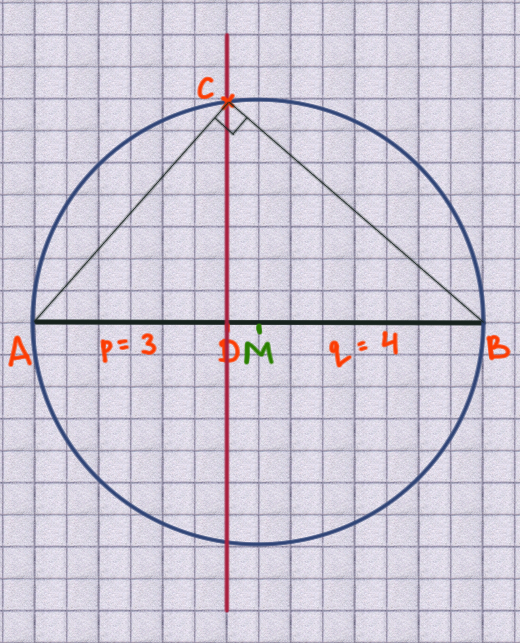
Measure the length of the line segment $\overline{DC}$.

The length is equal to $\sqrt{12}$. Why?

Because $h^2 = pq$ and therefore the height CD is equal to $h = \sqrt{pq}$.

This is known as the geometric mean or “Der Höhensatz” in German.

Geogebra App

here is a Geogebra App