introduction - exponential growth
unlimited growth and decay
growth - eaxample bacteria 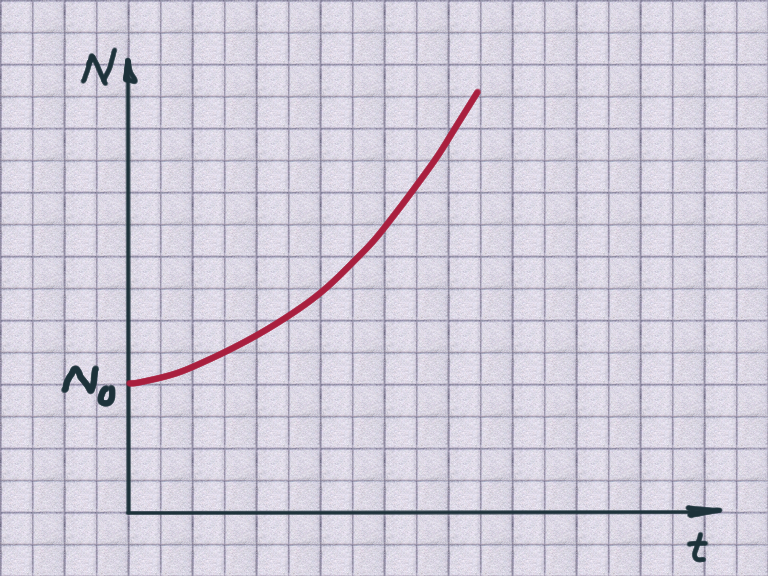
$${N(t) = N_0 \cdot \mathrm{e}^{kt}}$$
$N_0$: the initial amount at $t=0$.
time for initial amount to double - Verdopplungszeit
$T_2 = \frac{\ln 2}{k}, \,\, k>0$
radioactive decay 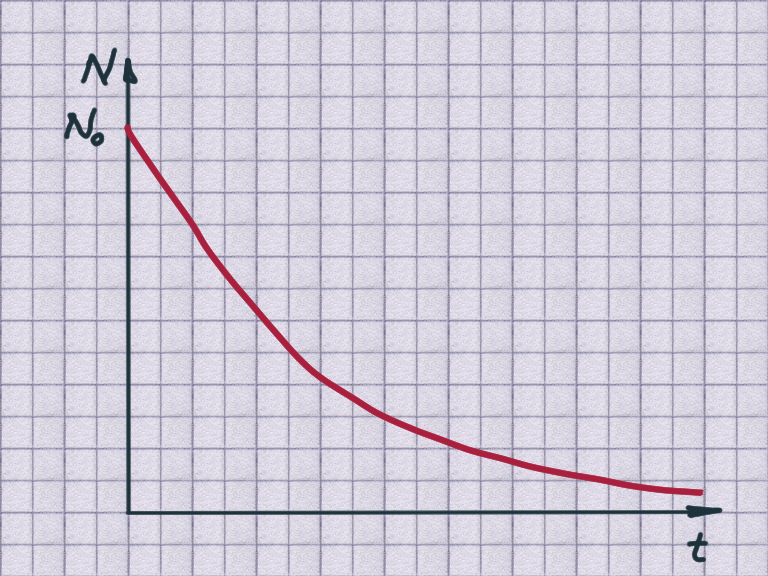
$${N(t) = N_0 \cdot \mathrm{e}^{-kt}}$$
$N_0$: the initial amount at $t=0$.
half-life - Halbwertszeit
$T_{\frac{1}{2}} = \frac{\ln (\frac{1}{2})}{-k}, \,\, k>0$
limited growth 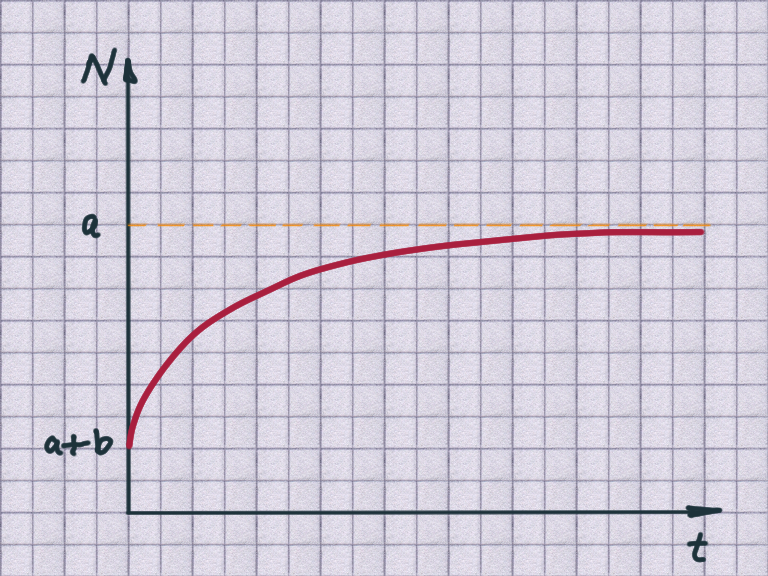
$${N(t) = a + b \cdot \mathrm{e}^{-kt}}$$
where $k>0$
$N_0 = a + b$: the initial amount.
$a$: the maximum possible amount as $t \rightarrow \infty$
limited decay - Newton’s equation of cooling 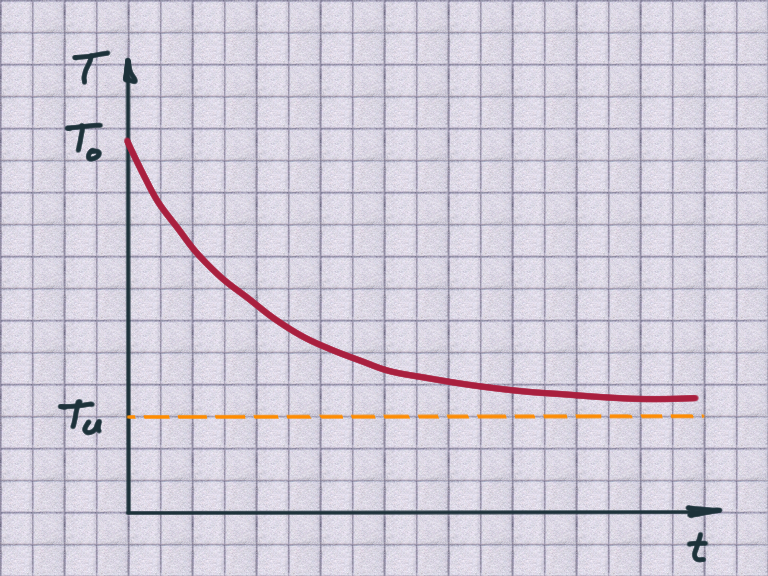
$${T(t) = T_U + c \cdot \mathrm{e}^{-kt}}$$
where $k>0$
$c = T_0 - T_U$
$T_0$ : the initial temperature at $t=0$
$T_U$ : temperature of the environment (Umgebungstemperatur) $t \rightarrow \infty$
combining the two - logistic growth
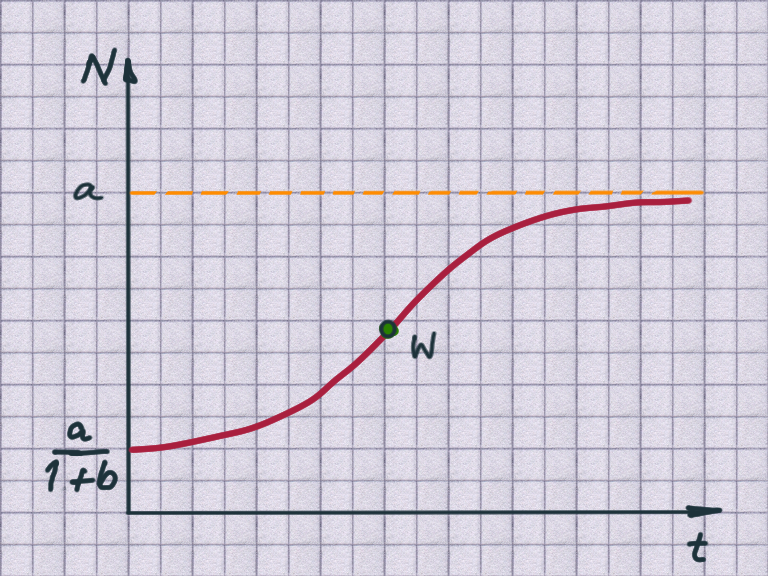
the logistic function in general terms
The logistic function N(t) is described by the parameters a, b and k. You can find the first and second derivative by using the quotient rule and the chain rule.
$${N(t) = \frac{a}{1 + b \cdot \mathrm{e}^{-kt}}}$$
where $k>0$
$N_0 = \frac{a}{1 + b}$: the initial amount.
$G = a$: the maximum possible amount as $t \rightarrow \infty$ (Grenzbestand)
$W$ : the point of inflexion - der Wendepunkt (maximum gradient / maximale Steigung)
the first and second derivative
$${N^\prime (t) = \frac{abk \cdot \mathrm{e}^{-kt}}{(1 + b \cdot \mathrm{e}^{-kt})^2}}$$
$${N^{\prime\prime} (t) = \frac{-abk^2 \cdot \mathrm{e}^{-kt} \left( 1 - b\mathrm{e}^{-kt}\right)}{(1 + b \cdot \mathrm{e}^{-kt})^3}}$$
other form
$${N(t) = \frac{N_0 \cdot G}{N_0 + (G - N_0) \cdot \mathrm{e}^{-Gkt}}}$$
logistic curve
the logistic curve is referred to as a common S-shaped curve (alos known as a sigmoid curve)