Hauptsatz der Integral- und Differenzialrechnung
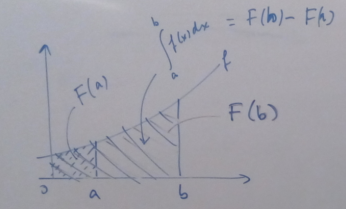
If $f$ is continuous on [a, b], and if $F$ is any antiderivative of $f$ on [a, b], then
$\int_{a}^{b} f(x)\ dx = F(b) - F(a)$
Note: in some books (UK) they write it as $\int_{a}^{b} f'(x)\ dx = f(b) - f(a) $ which is just another way to write it by denoting f(x) instead of F(x) and f’(x) instead of f(x).
proof
to do
or look here.